티스토리 뷰
programmers.co.kr/learn/courses/30/lessons/42839
코딩테스트 연습 - 소수 찾기
한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다. 각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이
programmers.co.kr
문제는 위와 같으며, 이 문제는 순열을 통해 해결하였습니다.
순열
순열은 서로 다른 n개의 수 중 r개를 나열하는 방법을 말합니다. 순열은 순서가 중요하기 때문에 [1,2,3] 중 [1,2]와 [2, 1]을 뽑는 경우는 다른 경우로 취급합니다. 순열 중 중복을 허용하여 자기 자신도 여러번 뽑을 수 있는 경우([1,2,3] 중 [1, 1]을 뽑는 경우)를 중복 순열이라고 합니다.
순열을 구하기 위해서는 각 자리 수를 직접 변경하는 swap 방식과 해당 위치의 수를 뽑았는지 아닌지를 판단하는 visited[] 배열을 사용하는 dfs 방식이 있지만 여기서는 dfs 방식만 살펴보겠습니다.
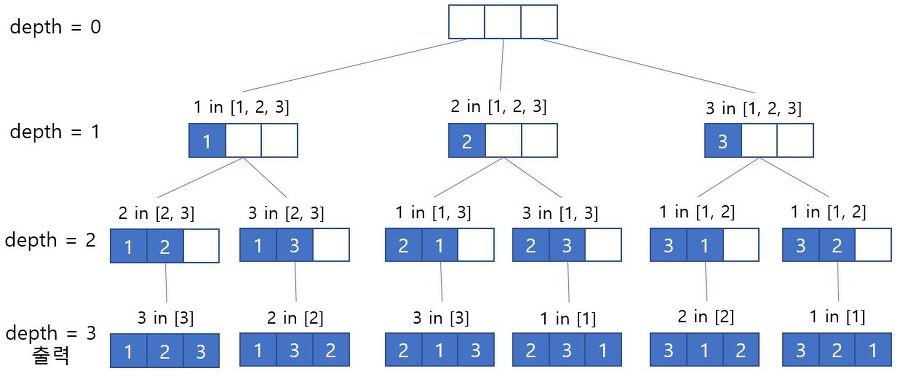
이 방법은 dfs를 수행하면서 각 depth마다 모든 인덱스를 확인하고 output 배열에 추가합니다. output 배열의 크기는 depth와 같습니다. output 배열에 값을 추가할 때 이미 선택된 인덱스의 값은 다시 추가하지 않습니다. 이미 선택이 되었는지 확인하기 위해 boolean 타입의 visited[] 배열을 사용합니다. depth의 값이 r 만큼이 되는 경우 output 배열에 들어있는 값이 최종 선택된 값들입니다.
이를 구현한 코드를 살펴보겠습니다.
// 순열 구하기
void permutation(int[] nums, int[] output, boolean[] visited, int depth, int n, int r) {
// r개의 수를 모두 고른 경우
if (depth == r) {
print(output);
return;
}
// 현재 depth에 들어갈 수를 처음 인덱스부터 끝까지 확인하면서
for (int i = 0; i < n; i++) {
// 해당 인덱스의 값이 이전에 선택되지 않은 경우
if (!visited[i]) {
visited[i] = true; // 선택한 것으로 하고
output[depth] = nums[i]; // 선택된 값을 output 배열에 추가
// 다음 depth 확인하기
permutation(nums, output, visited, depth + 1, n, r);
visited[i] = false; // 해당 인덱스 값을 선택하지 않은 것으로 변경
}
}
}
// output에 선택된 r개의 수 출력
void print(int[] output) {
for (int out : output) {
System.out.print(out + " ");
}
System.out.println();
}
/*
[입력] 3개([1, 2, 3]) 중 3개 뽑기
[출력]
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
*/
조합
조합은 서로 다른 n개의 수 중 r개 뽑는 방법을 말합니다. 순서가 중요하지 않기 때문에 [1,2,3] 중 [1,2]와 [2, 1]을 뽑는 경우를 같은 경우로 취급합니다. 조합 중에서도 중복을 허용하는 경우를 중복 조합이라고 합니다.
조합의 경우 순서가 없기 때문에 전체 인덱스를 돌면서 한 인덱스(i)를 선택하는 경우 다음 위치에는 뽑은 인덱스의 다음(i+1)부터 확인하면 됩니다. 이를 구현하기 위해 visited[] 배열과 start 변수를 사용하였습니다. 과정을 그림으로 간략히 살펴보면 다음과 같습니다.
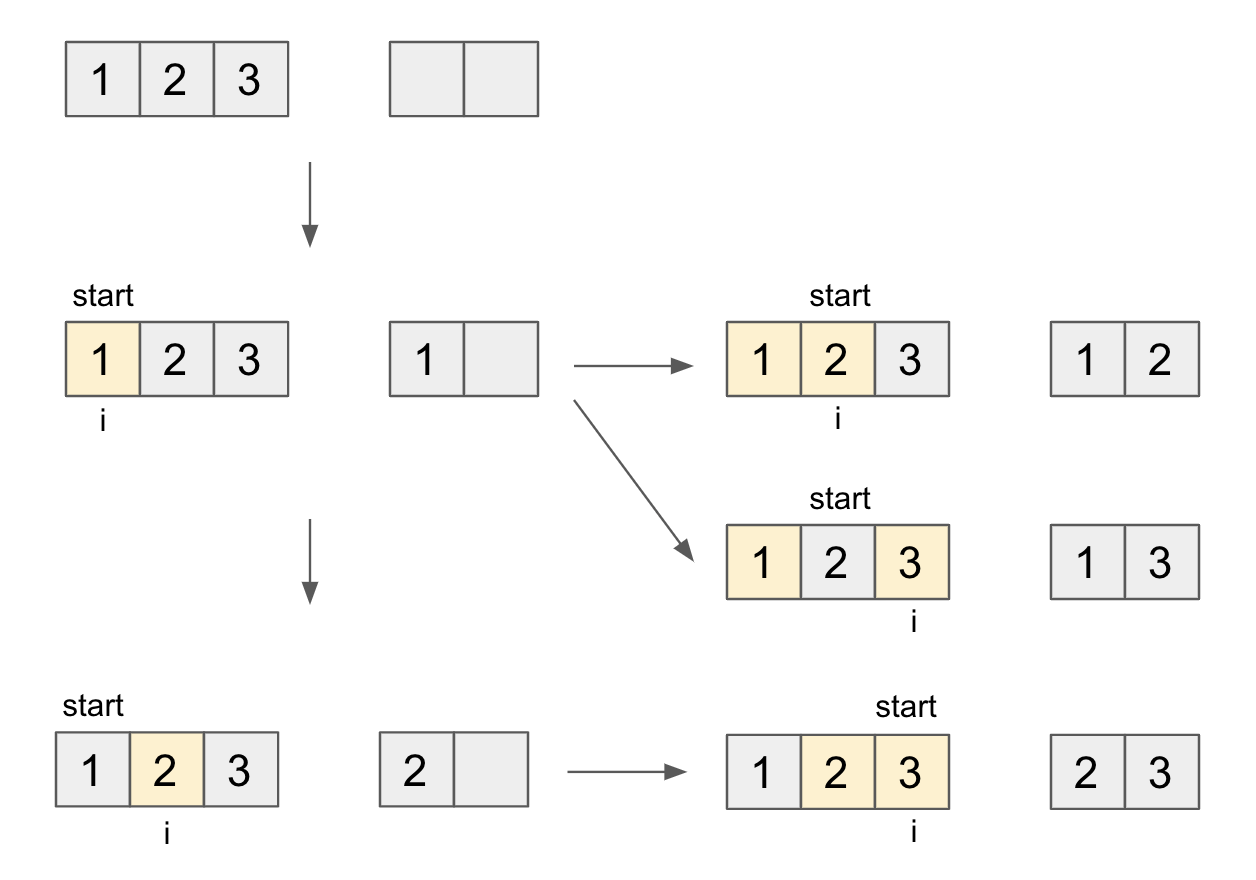
void combination(int[] nums, boolean[] visited, int start, int n, int r) {
// r개의 데이터를 모두 선택한 경우
if (r == 0) {
print(nums, visited);
return;
}
for (int i = start; i < n; i++) {
visited[i] = true; // i번째 수를 뽑는 경우
combination(nums, visited, i + 1, n, r - 1);
visited[i] = false; // i번째 수를 뽑지 않는 경우
}
}
void print(int[] nums, int[] visited) {
for(int i = 0; i < visited.length; i++) {
if (visited[i]) {
System.out.print(nums[i] + " ");
}
}
System.out.println();
}
/*
[입력] 3개([1, 2, 3]) 중 2개 뽑기
[출력]
1 2
1 3
2 3
*/다시 문제를 살펴보겠습니다.
주어진 문자열을 한글자씩 잘라서 숫자로 보고 해당 숫자들을 조합하여 만들 수 있는 소수를 구하는 문제였습니다. 이때 소수의 자릿수는 정해지지 않았기 때문에 모든 자릿수의 소수들을 확인해야합니다.
1. 길이가 n인 문자열이 주어지면 한글자씩 잘라 길이가 n인 int[] 배열에 추가합니다. ("17" => [1, 7])
2. 길이가 1부터 n까지 자릿수의 숫자를 모두 확인해야하므로 1부터 n까지 반복(i 변수 반복)하면서
3. n개의 숫자 중 i 길이의 숫자를 순열로 뽑습니다.
4. 순열을 구할 때 i 만큼 선택된 각 숫자들을 순서대로 붙여 i 자릿수의 숫자를 만들고 이 숫자들을 Set 에 저장합니다. 숫자 조합으로 만들어지는 최종 숫자의 중복을 피하기 위해 Set을 사용하였습니다.
5. i 자릿수의 숫자 모음인 Set에서 하나씩 숫자를 뽑아 소수인지 확인하고 소수인 경우 answer 값을 증가시킵니다.
6. 모든 자릿수의 숫자를 만들고 소수인지 확인이 끝나면 answer 를 반환합니다.
자바 코드는 다음과 같습니다.
import java.util.Arrays;
import java.util.HashSet;
import java.util.Set;
class Solution {
private static final Set<Integer> selectedCombi = new HashSet<>();
public int solution(String numbers) {
int answer = 0;
int[] nums = Arrays.stream(numbers.split("")).mapToInt(Integer::parseInt).toArray();
for(int i = 1; i <= nums.length; i++) {
selectedCombi.clear();
permutation(nums, new int[nums.length], new boolean[nums.length], 0, nums.length, i);
for (int num : selectedCombi) {
// 소수인지 확인하고 소수이면 answer 증가
if (isPrimeNumber(num)) {
answer++;
}
}
}
return answer;
}
// 순서를 지키면서 n 개중에서 r 개를 뽑는 경우
// 사용 예시: permutation(arr, output, visited, 0, n, 3);
static void permutation(int[] arr, int[] output, boolean[] visited, int depth, int n, int r) {
// r개의 숫자를 모두 선택한 경우
if (depth == r) {
int[] result = Arrays.copyOfRange(output, 0, depth);
// 숫자 만들어서 set에 추가하기
int newNum = makeNum(result);
selectedCombi.add(newNum);
return;
}
for (int i = 0; i < n; i++) {
if (!visited[i]) {
visited[i] = true;
output[depth] = arr[i];
permutation(arr, output, visited, depth + 1, n, r);
visited[i] = false;;
}
}
}
// 주어진 int[]의 순서대로 하나의 수 만들기
private static int makeNum(int[] nums) {
int result = 0;
for (int i = 0; i < nums.length; i++) {
result += nums[i] * Math.pow(10, nums.length - (i + 1));
}
return result;
}
// 소수인지 판단하기
private static boolean isPrimeNumber(int num) {
if (0 == num || 1 == num) {
return false;
}
for (int i = 2; i*i <= num; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
}'알고리즘' 카테고리의 다른 글
| [프로그래머스] 조이스틱 (0) | 2021.04.09 |
|---|---|
| [프로그래머스] 삼각 달팽이 (0) | 2021.04.08 |
| [프로그래머스] 더 맵게 (0) | 2021.04.05 |
| [프로그래머스] 네트워크 (0) | 2021.04.02 |
| [프로그래머스] 주식 가격 (0) | 2021.04.02 |
- Total
- Today
- Yesterday
- map
- 순열
- CodePipeline
- ECR
- programmers
- array
- ionic
- Combination
- CodeCommit
- sort
- java
- CodeDeploy
- Baekjoon
- 조합
- BFS
- 프로그래머스
- SWIFT
- EC2
- 소수
- cloudfront
- Dynamic Programming
- AWS
- Algorithm
- 수학
- 에라토스테네스의 체
- search
- spring
- string
- DFS
- permutation
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
